Uji F Simultan dalam Analisis Regresi Linear Berganda
Setelah sebelumnya kita melakukan pengujian hipotesis penelitian menggunakan metode analisis regresi linear berganda dengan software SPSS. Selanjutnya untuk interpretasi hasil analisis tersebut supaya lebih dipahami, maka perlu dilakukan uji F, uji t, dan koefisien determinasi untuk melihat kontribusi pengaruh (sumbangan efektif dan sumbangan relative) yang diberikan variabel independent (X) terhadap variabel dependent (Y).
Perbedaan antara uji F dan uji t dalam analisis regresi linear berganda adalah terletak pada makna pengaruh yang diberikan variabel X terhadap variabel Y apakah secara simultan (bersama-sama) atau parsial (sendiri-sendiri). Uji F memiliki tujuan untuk mengetahui pengaruh variabel X terhadap variabel Y secara simultan. Sedangkan uji t bertujuan untuk mengetahui pengaruh variabel X terhadap variabel Y secara parsial.
Contoh Kasus Analisis Regresi Linear Berganda
Kasus yang digunakan untuk uji F simultan adalah sama seperti artikel sebelumnya, yakni kasus saat membahas tutorial “Analisis Regresi Linear Berganda”. Dalam artikel tersebut, kita ingin menguji apakah terdapat pengaruh antara Tinggi Badan dan Jam Tidur terhadap Berat Badan.
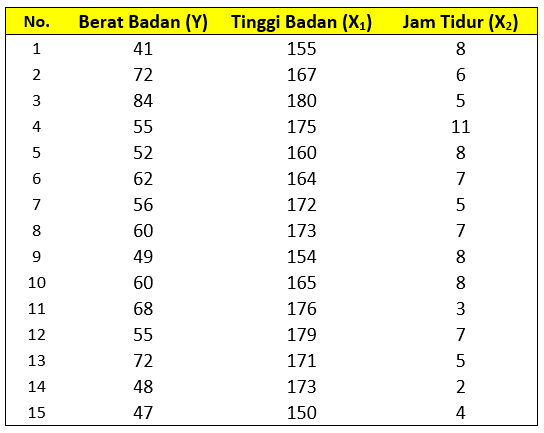
Berdasarkan contoh kasus di atas, maka uji F berguna untuk menguji apakah terdapat pengaruh Tinggi Badan dan Jam Tidur secara simultan (bersama-sama) terhadap Berat Badan. Sedangkan uji t berguna untuk menguji apakah terhadap pengaruh antara Tinggi Badan dan Jam Tidur secara parsial (terpisah) terhadap Berat Badan.

Catatan: Untuk melakukan uji F Simultan dalam analisis regresi linear berganda, maka kita cukup memperhatikan hasil yang terdapat dalam tabel output “ANOVA”.
Rumusan Hipotesis dalam Uji F Simultan
Adapun hipotesis (dugaan) yang diajukan dalam uji F Simultan adalah sebagai berikut:
H0 : tidak terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan dan Jam Tidur terhadap Berat Badan.
H1 : terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan dan Jam Tidur terhadap Berat Badan.
Dasar Pengambilan Keputusan dalam Uji F Simultan
Ada du acara yang bisa digunakan sebagai acuan atau pedoman untuk melakukan uji hipotesis dalam uji F Simultan. Pertama adalah dengan membandingkan nilai signifikan (Sig.) atau nilai probabilitas hasil output ANOVA. Kedua adalah dengan membandingkan nilai F hitung dengan nilai F tabel.
A. Berdasarkan Nilai Signifikan (Sig.) dari Ouput ANOVA
- Jika nilai Sig. < 0,05, maka H0 ditolak. Artinya, terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan (X1) dan Jam Tidur (X2) terhadap Berat Badan (Y).
- Jika nilai Sig. > 0,05, maka H0 tidak ditolak. Artinya, tidak terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan (X1) dan Jam Tidur (X2) terhadap Berat Badan (Y).
B. Berdasarkan Perbandingan Nilai F Hitung dengan F Tabel
- Jika nilai F hitung > F tabel, maka H0 ditolak. Artinya, terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan (X1) dan Jam Tidur (X2) terhadap Berat Badan (Y).
- Jika nilai F hitung < F tabel, maka H0 tidak ditolak. Artinya, tidak terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan (X1) dan Jam Tidur (X2) terhadap Berat Badan (Y).
Catatan: dasar pengambilan A dan B di atas, memiliki tingkat akurasi yang sama. Jadi boleh memilih salah satu saja, berdasarkan nilai F hitung atau nilai signifikansi. Karena jika nilai F hitung lebih besar dari F tabel, maka otomatis nilai Signifikansi (Sig.) yang dihasilkan output SPSS sudah pasti lebih kecil dari 0,05. Artinya, dari kedua dasar pengambilan keputusan tersebut akan menghasilkan kesimpulan yang sama dan tidak berseberangan satu sama lainnya.
Pengambilan Keputusan Uji F Simultan dalam Analisis Regresi Linear Berganda

A. Berdasarkan Nilai Signifikan (Sig.) dari Ouput ANOVA
Berdasarkan tabel output SPSS di atas, diketahui nilai Sig. adalah sebesar 0,064. Karena Sig. 0,064 > 0,05, maka sebagaimana dasar pengambilan keputusan dalam uji F Simutan dapat disimpulkan bahwa Tinggi Badan (X1) dan Jam Tidur (X2) tidak terdapat pengaruh yang signifikan secara simultan terhadap Berat badan (Y).
B. Berdasarkan Perbandingan Nilai F Hitung dengan F Tabel
Berdasarkan tabel output SPSS di atas, diketahui nilai F hitung adalah sebesar 3,479. Karena nilai F hitung 3,479 < 3,81, sebagaimana dasar pengambilan keputusan dalam uji F Simultan dapat disimpulkan bahwa Tinggi Badan (X1) dan Jam Tidur (X2) tidak terdapat pengaruh yang signifikan secara simultan terhadap Berat badan (Y).
Catatan: F tabel dicari pada distribuni nilai r tabel statistik pada signifikansi 5% atau 0,05 dengan menggunakan rumus F tabel = (k ; n-k). dimana “k” adalah jumlah variabel independent (variabel bebas atau X), sedangkan “n” adalah jumlah responden atau jumlah sampel penelitian. Dalam penelitian ini jumlah “k” adalah 2 yakni variabel Tinggi Badan (X1) dan variabel Jam Tidur (X2). Sedangkan jumlah “n” adalah 15 orang mahasiswa (responden). Selanjutnya nilai ini kita masukkan ke dalam rumus, maka menghasilkan angka (2 ; 15-2) = (2 ; 13). Angka ini akan dijadikan acuan untuk mencari atau melihat nilai F tabel pada distribusi nilai F tabel statistik. Maka ditemukan nilai F tabel adalah sebesar 3,81. Lihat gambar di bawah ini.

Kesimpulan: berdasarkan kedua pembahasan dalam uji F Simultan di atas, maka dapat kita simpulkan bahwa tidak terdapat pengaruh yang signifikan secara simultan pada Tinggi Badan dan Jam Tidur terhadap Berat Badan.
Setelah kita ketahui bahwa tidak terdapat pengaruh simultan, maka selanjutnya kita akan mencari berapa % pengaruh yang diberikan kedua variabel tersebut secara simultan. Adapun materi tentang artikel ini akan kita bahas pada artikel selanjutnya.
Demikian pembahasan kali ini mengenai cara melakukan uji F simultan dalam analisis regresi linear berganda dengan software SPSS. Semoga bermanfaat dan terima kasih.